Esse é um texto traduzido, publicado originalmente na revista Forbes e possui autoria do astrofísico Ethan Siegel

Na semana passada [texto de abril de 2018], o Instituto Perimeter de Física Teórica publicou um artigo onde perguntaram a 14 cientistas qual era a sua equação favorita e por quê. Houve muitas boas respostas de muitas áreas diferentes de pesquisa, da termodinâmica à matemática pura. Muitas pessoas seguiram com equações fundamentais, como a lei da gravidade, a famosa F = ma de Newton ou a equação de Schrödinger, que governa as partículas quânticas. Eu tive a honra de ser incluído nesta lista, e a resposta que dei não foi nada disso. Em vez disso, a equação que escolhi foi muito específica: a primeira equação de Friedmann, derivada da Relatividade Geral de Einstein sob um conjunto específico de circunstâncias.

Quando perguntaram por que eu escolhi essa equação, eu disse:
“A primeira equação de Friedmann descreve como, com base no que está no universo, sua taxa de expansão [do universo] mudará com o tempo. Se você quer saber de onde o Universo veio e para onde está indo, tudo o que você precisa medir é como ele está se expandindo hoje e o que está nele. Essa equação permite prever o resto!”
A história de Friedmann, sua equação e o que ela nos ensina sobre o nosso Universo é uma história que todo entusiasta da ciência deveria conhecer.
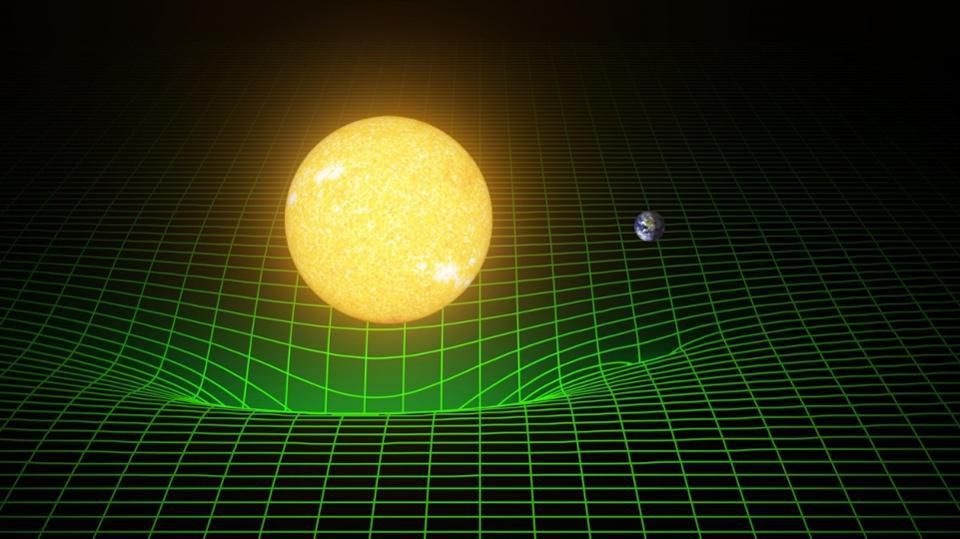
Em 1915, Einstein apresentou sua Teoria da Relatividade Geral, que relacionava a curvatura do espaço-tempo, por um lado, à presença de matéria e energia no Universo, por outro. Como John Wheeler observou muitos anos depois, o espaço-tempo diz como a matéria deve se movimentar; a matéria diz ao espaço-tempo como se curvar. A teoria de Einstein, de uma só vez, reproduziu todos os sucessos anteriores da gravidade de Newton, explicou as complexidades da órbita de Mercúrio (que a teoria de Newton não conseguia) e fez uma nova previsão para a curvatura da luz das estrelas, espetacularmente confirmada durante o eclipse solar total de 1919. O único problema? A fim de evitar que o Universo entrasse em colapso sobre si mesmo, Einstein precisou acrescentar uma constante cosmológica — uma correção ad hoc para o fato de os espaços-tempos estáticos serem instáveis na Relatividade Geral — à sua teoria. Era feia, conveniente e não tinha outra motivação.

Entra Friedmann. Em 1922, apenas três anos após a confirmação do eclipse, Friedmann encontrou uma maneira elegante de salvar o universo e, ao mesmo tempo, eliminou a constante cosmológica: não assuma que ele [o universo] é estático. Em vez disso, argumentou Friedmann, suponha que é como observamos, cheio de matéria e radiação, e passível de ser curvo. Suponha, ainda, que seja aproximadamente isotrópico e homogêneo, que são palavras matemáticas que significam “o mesmo em todas as direções” e “o mesmo em todos os lugares”. Se você fizer essas suposições, duas equações aparecem: as equações de Friedmann. Elas dizem que o Universo não é estático, mas sim que ele se expande ou se contrai, dependendo da taxa de expansão e do conteúdo do seu Universo. Melhor de tudo, elas dizem como o Universo evolui com o tempo, arbitrariamente longe no futuro ou no passado.
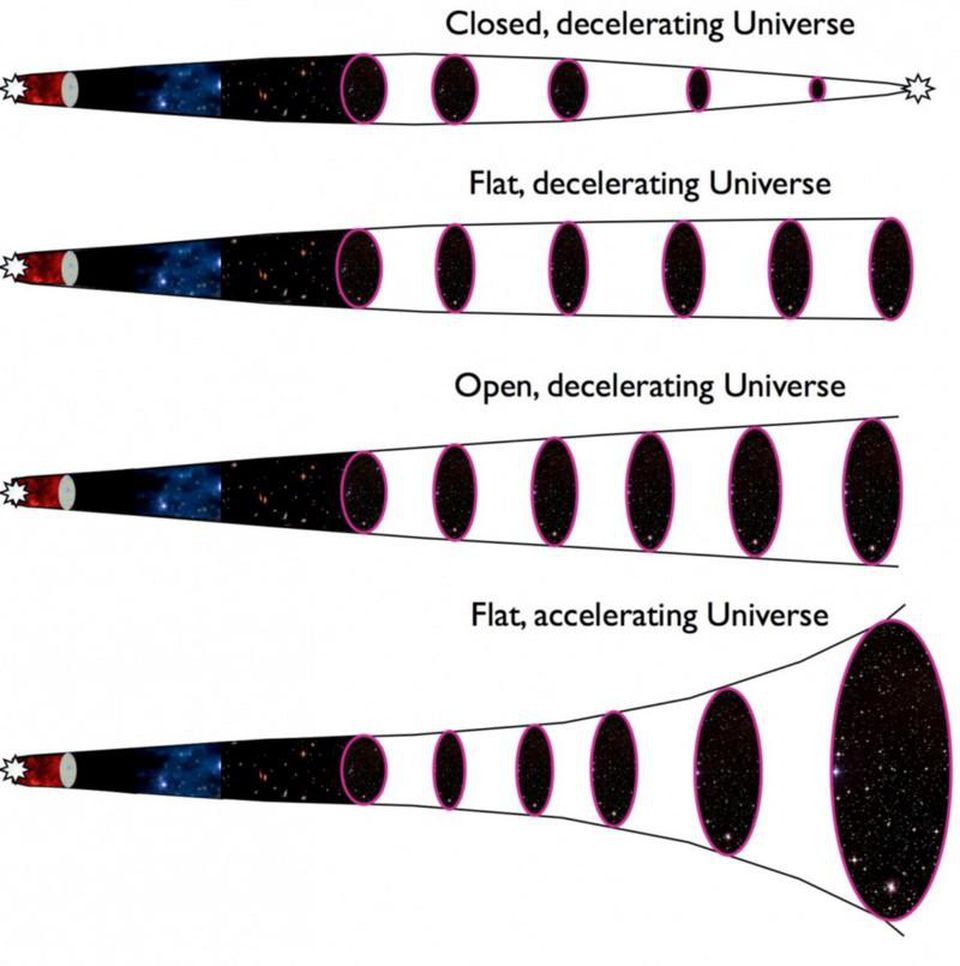
O que é notável é que Friedmann explicou isso antes de descobrirmos que o Universo estava se expandindo; antes que Hubble descobrisse que havia galáxias além da Via Láctea no Universo! Não seria até o próximo ano, em que o Hubble identificaria as estrelas variáveis do tipo Cefeida [2] em Andrômeda, ensinando-nos a sua distância e colocando-a longe de nossa própria galáxia. Além disso, não seria até o final da década de 1920 que Georges Lemaître e, mais tarde, independentemente, Hubble, colocariam as imagens de desvios para o vermelho e distantes juntas para concluir que o Universo estava se expandindo. Naquela época, o jovem Friedmann já havia morrido tragicamente de febre tifoide, que contraiu quando retornava de sua lua de mel em 1925.

No entanto, seu legado científico era indiscutível e se tornou ainda mais quando entendemos melhor a cosmologia. A primeira equação de Friedmann é a mais importante das duas, já que é a mais fácil e direta de se relacionar às observações. De um lado, você tem o equivalente da taxa de expansão (ao quadrado) ou o que é coloquialmente conhecido como a constante de Hubble (não é verdadeiramente uma constante, uma vez que pode mudar à medida que o Universo se expande ou se contrai ao longo do tempo). Isso nos diz como o tecido do Universo se expande ou se contrai em função do tempo.
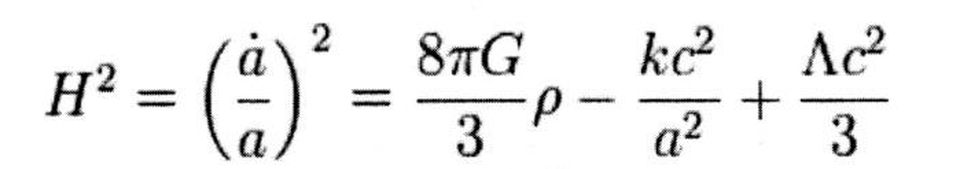
Do outro lado está literalmente todo o resto. Há toda a matéria, radiação e quaisquer outras formas de energia que compõem o Universo. Há a curvatura intrínseca ao espaço em si, dependendo se o Universo está fechado (curvado positivamente), aberto (curvado negativamente) ou plano (sem curvatura). E há também o termo “Λ”: uma constante cosmológica, que pode ser uma forma de energia ou pode ser uma propriedade intrínseca do espaço.
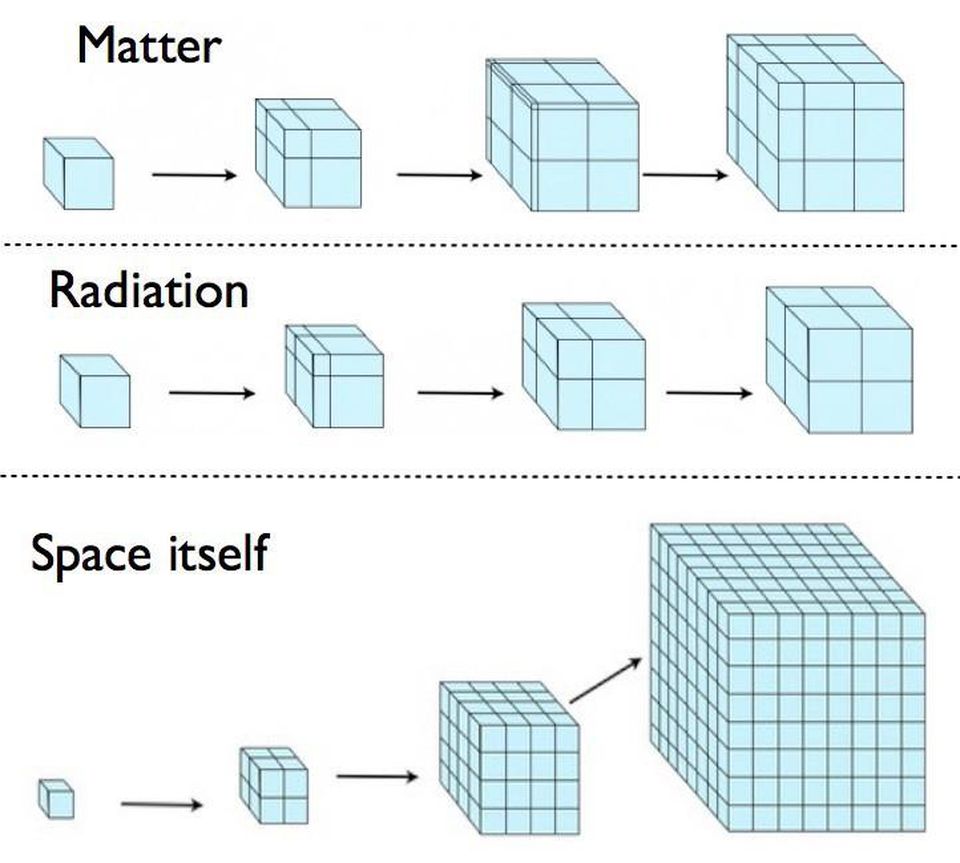
De qualquer maneira, esta é a equação que relaciona como o Universo se expande, quantitativamente, para o que compõe a matéria e a energia dentro dele. Meça o que está no seu Universo hoje e quão rápido ele está se expandindo hoje, e você pode extrapolar para frente ou para trás em quantidades arbitrárias. Você pode saber como o Universo estava se expandindo no passado distante ou imediatamente após o Big Bang. Você pode saber se vai colapsar novamente ou não (não vai), se a taxa de expansão vai “assintotar” a zero (não vai) ou permanecer positiva para sempre (vai).
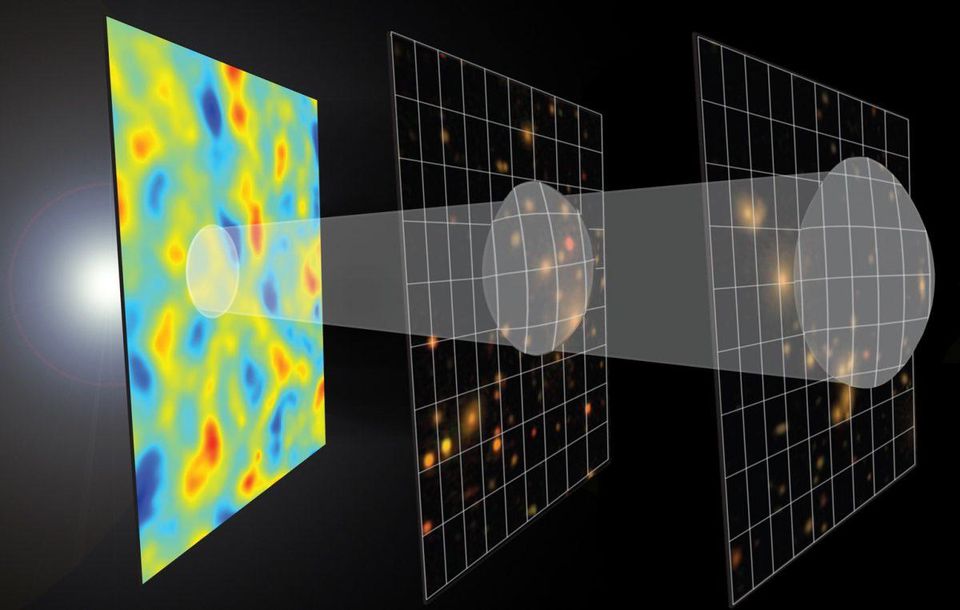
E talvez de forma mais espetacular, você pode adicionar imperfeições sobre esse fundo suave. As imperfeições de densidade que você coloca no seu Universo lhe dizem como a estrutura em grande escala cresce e se forma, o que se transformará em uma galáxia/aglomerado e o que não será, e o que se tornará vinculado gravitacionalmente versus o que será separado.
Tudo isso pode ser derivado de uma única equação: a primeira equação de Friedmann.
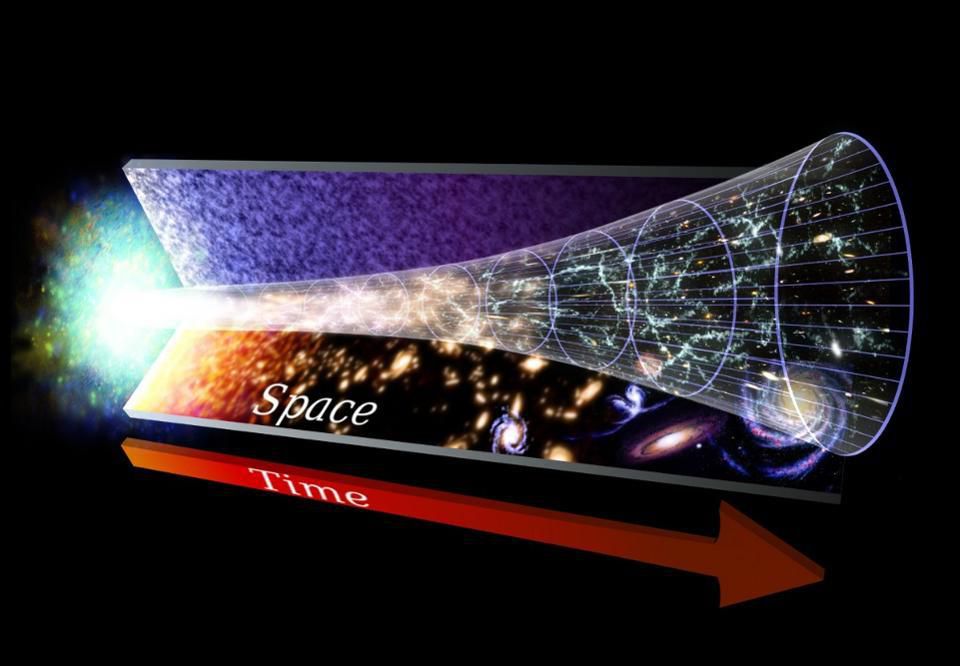
Embora a vida de Friedmann tenha sido curta, sua influência não pode ser exagerada. Ele foi o primeiro a derivar a solução da Relatividade Geral que descreve nosso Universo: um Universo em expansão cheio de matéria. Embora tenha sido derivada de forma independente, mais tarde, por outros três — Georges Lemaître, Howard Robertson e Arthur Walker — Friedmann percebeu plenamente suas implicações e aplicações, e chegou a apresentar as primeiras soluções para espaços curvos exóticos. Ele era um professor influente também; seu aluno mais famoso foi George Gamow, que mais tarde viria a aplicar o trabalho de Friedmann ao Universo em expansão para criar a Teoria do Big Bang de nossa origem cósmica.
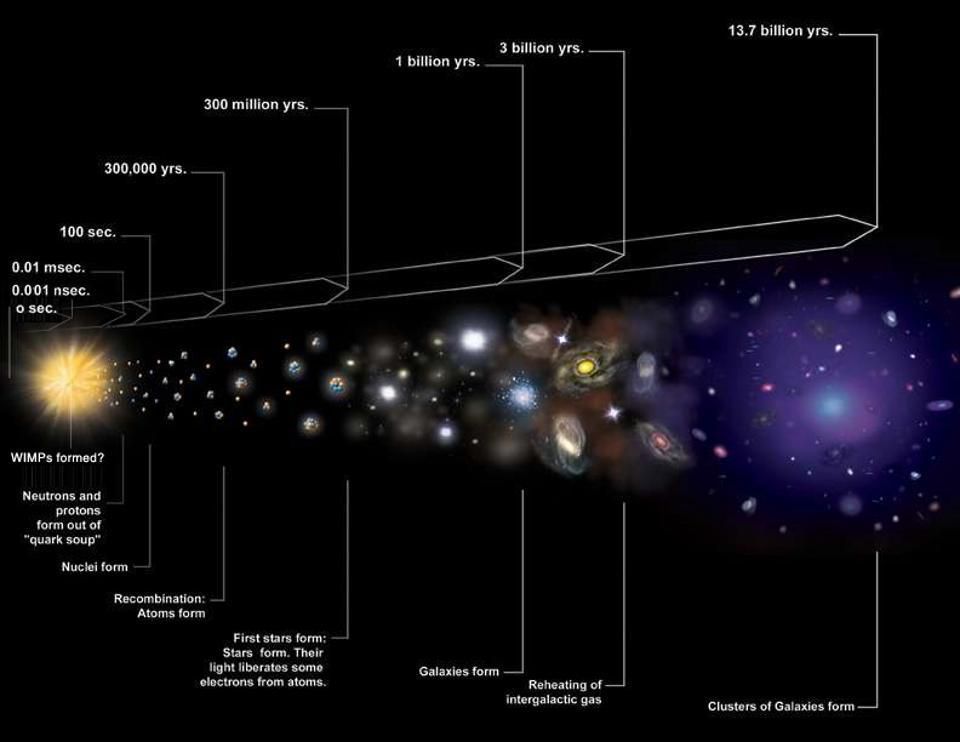
Quase um século depois de sua obra mais famosa, as equações de Friedmann foram estendidas a um Universo contendo uma origem inflacionária, matéria escura, neutrinos e energia escura. No entanto, elas ainda são perfeitamente válidas, sem adições ou modificações necessárias para explicar esses avanços tremendos. Embora todos possamos discutir sobre os méritos relativos de Einstein, Newton, Maxwell, Feynman, Boltzmann, Hawking e muitos outros, quando se trata do Universo em expansão, a primeira equação de Friedmann é a única que você precisa. Ela conecta a matéria e a energia que estão presentes à taxa de expansão hoje, no passado e no futuro, e permite que você conheça o destino e a história do Universo a partir de medições que podemos fazer hoje. No que diz respeito ao tecido do nosso Universo, esta equação leva a coroa como a mais importante.
Notas do tradutor
- Uma das características que difere a Teoria da Relatividade Geral (TRG) da Teoria da Relatividade Restrita (TRR) é a necessidade de considerar a interação gravitacional nos sistemas e, consequentemente, nas equações. Podemos pensar na TRG como uma generalização da TRR que considera a curvatura do espaço-tempo e sua interação gravitacional entre os corpos que possuem massa. Portanto, quando estudamos um corpo de baixa interação gravitacional, em outras palavras, corpos pequenos e sem muita massa, com quase nenhum campo gravitacional, podemos tentar descrevê-lo utilizando a TRR, não sendo necessário, portanto, utilizar a TRG. É sobre essa aproximação matemática que o Ethan está chamando de “limite de campo fraco”. As equações não são triviais, mas você pode iniciar no Wikipedia, no tópico “Definição e aplicações básicas”.
- Cefeida é um tipo de estrela gigante, classificada como “estrela variável pulsante”, que possui variações em sua luminosidade em intervalos de tempo (período) muito bem definidos. Saiba mais.
O objetivo das traduções é tornar acessível conteúdos e discussões que possam fomentar ainda mais nosso cenário científico, principalmente para quem está iniciando os estudos. Qualquer crítica ou sugestão é só entrar em contato. Para acessar todas as Traduções, clique aqui.




Deixe um comentário